Steady Buoyant Navier-Stokes for Differentially Heated Cavity
The Differentially Heated Cavity is taken from the ROSE-ROM4FOAM tutorial. It’s 2D Cavity with velocity imposed at the left and right boundary, along with [Sah18].
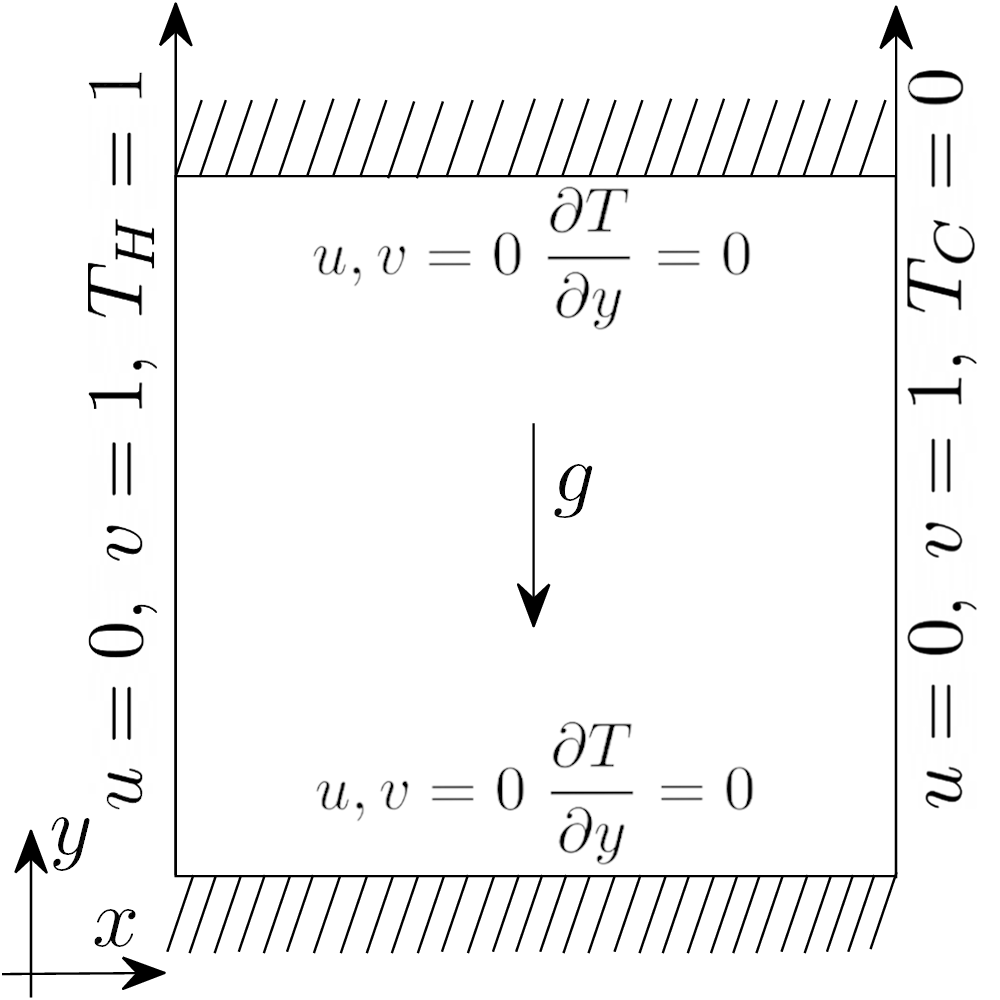
The governing equations are the Navier-Stokes with energy equation under the Boussinesq approximation
\[\begin{split}\left\{ \begin{aligned}
\nabla \cdot \mathbf{u}&=0 \quad &\text{ in } \Omega\\
(\mathbf{u} \cdot \nabla)\mathbf{u} - \nu \Delta \mathbf{u}+ \nabla p - \mathbf{g}\cdot\beta(T-T_\infty) &=0 & \text{ in } \Omega \\
\mathbf{u} \cdot \nabla T - \alpha \Delta T&= 0\quad& \text{ in } \Omega
\end{aligned} \right.\end{split}\]
given \(\Omega\) as the domain.