Unsteady Laminar Navier Stokes - DFG2 benchmark

Aim of this tutorial: learn how to generate time-dependent snapshots, create the reduced space using POD and perform the online phase with POD with Interpolation (POD-I).

The DFG2 benchmark is taken from the FeatFlow Repository. It’s a 2D version of a Flow Over Cylinder Problem, able to observe Von-Karman vortex shedding.

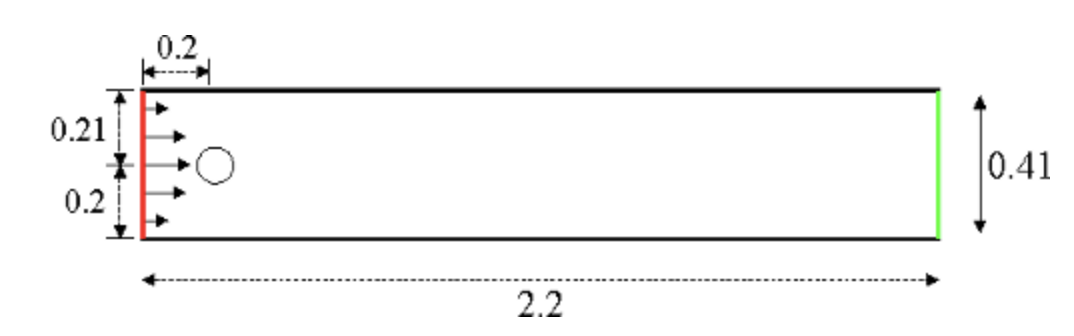
The governing equations are the Navier Stokes equations:

\[\begin{split}\left\{ \begin{array}{ll} \nabla\cdot \mathbf{u} = 0 & \mathbf{x}\in\Omega\\ \frac{\partial \mathbf{u}}{\partial t} + \left(\mathbf{u}\cdot \nabla\right)\mathbf{u} -\nu \Delta \mathbf{u} + \nabla p = 0 & \mathbf{x}\in\Omega\\ \mathbf{u}=\mathbf{u}_{in},\;\; \frac{\partial p}{\partial \mathbf{n}} = 0 & \mathbf{x}\in\Gamma_{in} \\ \mathbf{u}=\mathbf{0},\;\; \frac{\partial p}{\partial \mathbf{n}} = 0 & \mathbf{x}\in\Gamma_{w} \\ \frac{\partial \mathbf{u}}{\partial \mathbf{n}}=0,\;\; p = 0 & \mathbf{x}\in\Gamma_{out} \end{array} \right.\end{split}\]

given \(\Omega\) as the domain and \(\partial\Omega\) as its boundary, composed by \(\partial\Omega = \Gamma_{in}\cup\Gamma_{w}\cup\Gamma_{out}\) where \(\Gamma_{in}\) is the inlet boundary, \(\Gamma_{w}\) is the wall boundary and \(\Gamma_{out}\) is the outlet.

Steps:

• Generation of the snapshots
  • Mesh generation
  • Physical and discretization parameters
  • Assembling variational forms
    • Setting up the tools to compute drag and lift coefficient
  • Solving the time-dependent problem
    • Comparison with benchmark data
• Offline Phase
  • Importing Snapshots
  • POD algorithm
    • Decay of the POD eigenvalues
    • Definition of the modes
    • Computing the training error
  • Generation of the maps
    • Linear Interpolation
    • Radial Basis Function Interpolation
    • Plotting the maps
  • Post Process: plotting the POD modes
• Online Phase: POD-I
  • Importing Snapshots and offline results
  • Online Phase
    • Test Error
    • Post Process