ANL11-A2: IAEA 2D PWR
This notebook implements a steady neutron diffusion equation on the ANL11-A2 benchmark, also referred to as IAEA benchmark using the FEniCSx library.
[2]:
from dolfinx.io import gmshio
import gmsh
from mpi4py import MPI
import numpy as np
import pandas as pd
from ufl import Measure
from IPython.display import clear_output
import matplotlib.pyplot as plt
from matplotlib import cm
import sys
mesh_path = '../../../mesh/'
benchmark_path = '../../../BenchmarkData/'
sys.path.append('../../../models/fenicsx')
Preamble
The geometry and the main physical parameters will be assigned.
Mesh Import
The geometry and the mesh are imported from “ANL11-A2_octave.msh”, generated with GMSH.
[3]:
gdim = 2
model_rank = 0
mesh_comm = MPI.COMM_WORLD
mesh_factor = .75
# Initialize the gmsh module
gmsh.initialize()
# Load the .geo file
gmsh.merge(mesh_path+'ANL11-A2_octave.geo')
gmsh.model.geo.synchronize()
gmsh.option.setNumber("Mesh.MeshSizeFactor", mesh_factor)
gmsh.model.mesh.generate(gdim)
gmsh.model.mesh.optimize("Netgen")
clear_output()
# Domain
domain, ct, ft = gmshio.model_to_mesh(gmsh.model, comm = mesh_comm, rank = model_rank, gdim = gdim )
gmsh.finalize()
domain1_marker = 10
domain2_marker = 20
domain3_marker = 30
domain4_marker = 40
boundary_marker = 1
tdim = domain.topology.dim
fdim = tdim - 1
ds = Measure("ds", domain=domain, subdomain_data=ft)
dx = Measure("dx", domain=domain)
domain.topology.create_connectivity(fdim, tdim)
Define parameter functions on the different regions
Since there are 4 subdomains in \(\Omega\) (i.e., fuel-1, fuel-2, fuel-rod, reflector) the values of the parameters changes according to the region, therefore proper functions should be defined.
[4]:
regions = [domain1_marker, domain2_marker, domain3_marker, domain4_marker]
neutronics_param = dict()
neutronics_param['Energy Groups'] = 2
neutronics_param['D'] = [np.array([1.5, 1.5, 1.5, 2.]),
np.array([0.4, 0.4, 0.4, 0.3])]
neutronics_param['xs_a'] = [np.array([0.01, 0.01, 0.01, 0.]),
np.array([0.085, 0.08, 0.13, 0.01])]
neutronics_param['nu_xs_f'] = [np.array([0., 0., 0., 0.]),
np.array([0.135, 0.135, 0.135, 0.])]
neutronics_param['chi'] = [np.array([1,1,1,1]),
np.array([0,0,0,0])]
neutronics_param['B2z'] = [np.array([0.8e-4]*4),
np.array([0.8e-4]*4)]
neutronics_param['xs_s'] = [[np.array([0]*4), np.array([0.02, 0.02, 0.02, 0.04])],
[np.array([0]*4), np.array([0]*4)]]
nu_value = 1
Ef = 1
reactor_power = 1
albedo = [0.4692] * 2
Solution of the eigenvalue problem
The MG diffusion equation is discretised using the Finite Element Method, and its eigenvalue formulation is solved through the standard inverse-power method.
[6]:
from neutronics.neutr_diff import steady_neutron_diff
neutr_steady_problem = steady_neutron_diff(domain, ct, ft, neutronics_param, regions, boundary_marker,
albedo = albedo)
neutr_steady_problem.assembleForm()
# Solving transient problem
phi_ss, k_eff = neutr_steady_problem.solve(power = reactor_power, Ef=Ef, nu = nu_value,
LL = 50, maxIter = 500, verbose=True)
Iter 050 | k_eff: 1.029513 | Rel Error: 4.444e-06
Iter 100 | k_eff: 1.029585 | Rel Error: 2.970e-07
Iter 150 | k_eff: 1.029591 | Rel Error: 3.668e-08
Iter 200 | k_eff: 1.029592 | Rel Error: 5.408e-09
Iter 250 | k_eff: 1.029592 | Rel Error: 8.227e-10
Iter 300 | k_eff: 1.029592 | Rel Error: 1.258e-10
Neutronics converged with 307 iter | k_eff: 1.02959182 | rho: 2874.13 pcm | Rel Error: 9.670e-11
Post-processing
The solution of the eigenvalue problem is compared with reference data.
Let us compare the \(k_{eff}\) with the benchmark value
[7]:
print('Computed k_eff = {:.5f}'.format(k_eff))
print('Benchmark k_eff = {:.5f}'.format(1.02959))
print('Relative error = {:.5f}'.format(np.abs(k_eff - 1.02959) / 1.02959 * 1e5)+' pcm')
Computed k_eff = 1.02959
Benchmark k_eff = 1.02959
Relative error = 0.17629 pcm
Let us plot the solution against benchmark data along the diagonal \(x=y\) and along the \(x\)-axis \(y=0\).
[10]:
from plotting import extract_cells
Nhplot = 1000
xMax = 170
x_line = np.linspace(0, xMax + 1e-20, Nhplot)
points = np.zeros((3, Nhplot))
points[0] = x_line
xPlot_0, cells_0 = extract_cells(domain, points)
points[1] = x_line
xPlot_1, cells_1 = extract_cells(domain, points)
## Uploading data from benchmark
x_axis_data = pd.read_excel(benchmark_path+'neutronics/ANL11-A2/data.xlsx', sheet_name='x-axis').to_numpy()/1000
diagonal_data = pd.read_excel(benchmark_path+'neutronics/ANL11-A2/data.xlsx', sheet_name='Diagonal').to_numpy()/1000
mark_size = 10
ls = 2
labelsize = 30
tickssize = 20
legend_size = 25
fluxFigure = plt.figure( figsize = (14,10) )
plt.subplot(2,2,1)
plt.plot(x_axis_data[:, 0], x_axis_data[:,1] / max(x_axis_data[:,1]), '^', c='orange',label = r'Argonne', markersize=mark_size)
plt.plot(xPlot_0[:,0], phi_ss[0].eval(xPlot_0, cells_0) / max(phi_ss[0].eval(xPlot_0, cells_0)), 'r', label = r'dolfinx', linewidth=ls)
plt.ylabel(r"$\tilde{\phi}_1$ at $y=0$",fontsize=labelsize)
plt.xticks(fontsize=tickssize)
plt.yticks(fontsize=tickssize)
plt.grid(which='major',linestyle='-')
plt.grid(which='minor',linestyle='--')
plt.legend(fontsize = legend_size, loc = 'lower left', framealpha=1)
plt.xlim(0, 170)
plt.ylim(0., 1.02)
plt.subplot(2,2,2)
plt.plot(x_axis_data[:, 0], x_axis_data[:,2] / max(x_axis_data[:,2]), '^', c='g',label = r'Argonne', markersize=mark_size)
plt.plot(xPlot_0[:,0], phi_ss[1].eval(xPlot_0, cells_0) / max(phi_ss[1].eval(xPlot_0, cells_0)), 'b', label = r'dolfinx', linewidth=ls)
plt.ylabel(r"$\tilde{\phi}_2$ at $y=0$",fontsize=labelsize)
plt.xticks(fontsize=tickssize)
plt.yticks(fontsize=tickssize)
plt.grid(which='major',linestyle='-')
plt.grid(which='minor',linestyle='--')
plt.legend(fontsize = legend_size, loc = 'lower left', framealpha=1)
plt.xlim(0, 170)
plt.ylim(0., 1.02)
plt.subplot(2,2,3)
plt.plot(diagonal_data[:, 0], diagonal_data[:,2] / max(diagonal_data[:,2]), '^', c='orange',label = r'Argonne', markersize=mark_size)
plt.plot(xPlot_1[:,0], phi_ss[0].eval(xPlot_1, cells_1) / max(phi_ss[0].eval(xPlot_1, cells_1)), 'r', label = r'dolfinx', linewidth=ls)
plt.xlabel(r"$y\,[cm]$",fontsize=labelsize)
plt.ylabel(r"$\tilde{\phi}_1$ at $y=x$",fontsize=labelsize)
plt.xticks(fontsize=tickssize)
plt.yticks(fontsize=tickssize)
plt.grid(which='major',linestyle='-')
plt.grid(which='minor',linestyle='--')
plt.legend(fontsize = legend_size, loc = 'lower left', framealpha=1)
plt.xlim(0, 140)
plt.ylim(0., 1.02)
plt.subplot(2,2,4)
plt.plot(diagonal_data[:, 0], diagonal_data[:,3] / max(diagonal_data[:,3]), '^', c='g',label = r'Argonne', markersize=mark_size)
plt.plot(xPlot_1[:,0], phi_ss[1].eval(xPlot_1, cells_1) / max(phi_ss[1].eval(xPlot_1, cells_1)), 'b', label = r'dolfinx', linewidth=ls)
plt.xlabel(r"$y\,[cm]$",fontsize=labelsize)
plt.ylabel(r"$\tilde{\phi}_1$ at $y=x$",fontsize=labelsize)
plt.xticks(fontsize=tickssize)
plt.yticks(fontsize=tickssize)
plt.grid(which='major',linestyle='-')
plt.grid(which='minor',linestyle='--')
plt.legend(fontsize = legend_size, loc = 'lower left', framealpha=1)
plt.xlim(0, 140)
plt.ylim(0., 1.02)
plt.tight_layout()
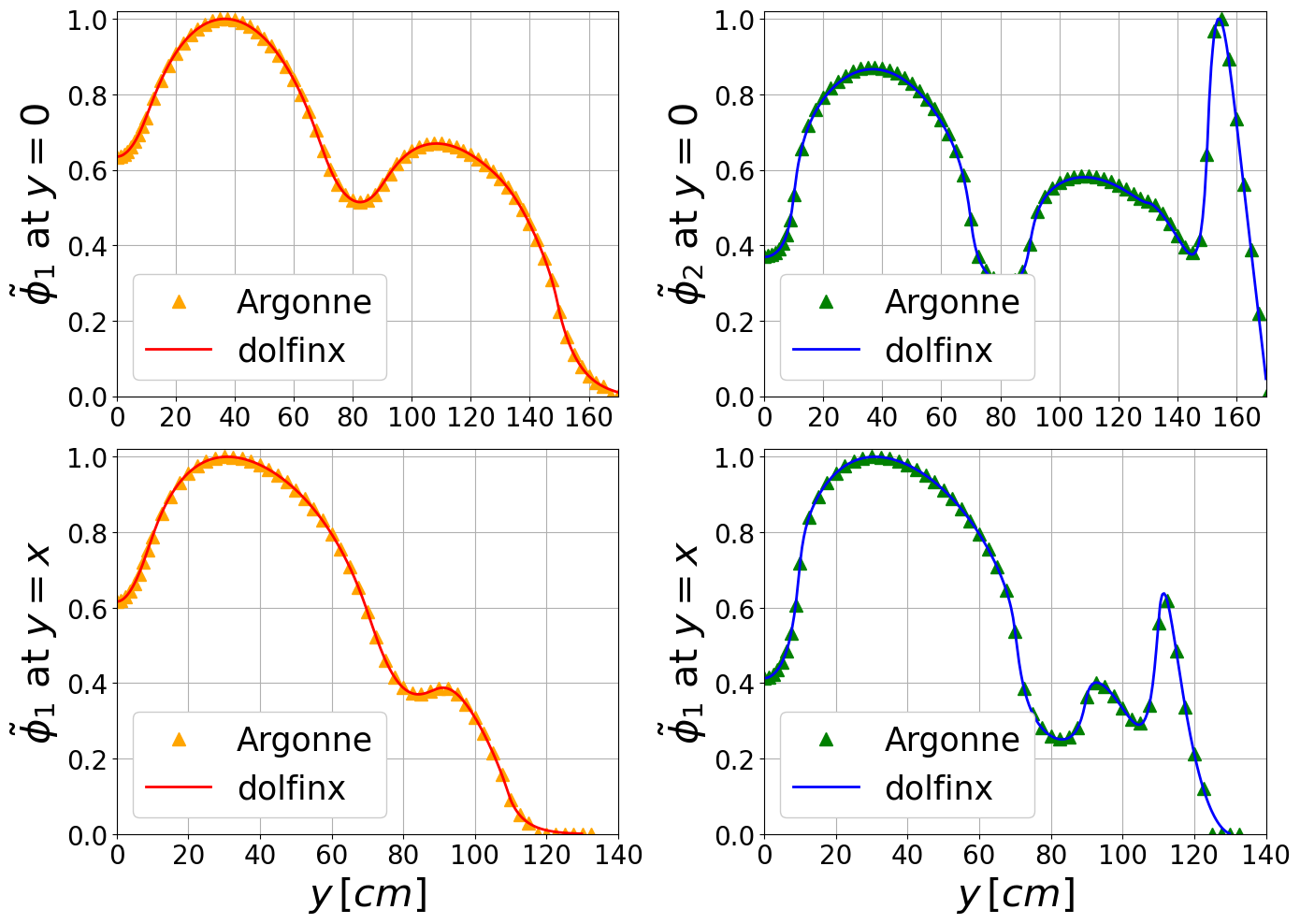
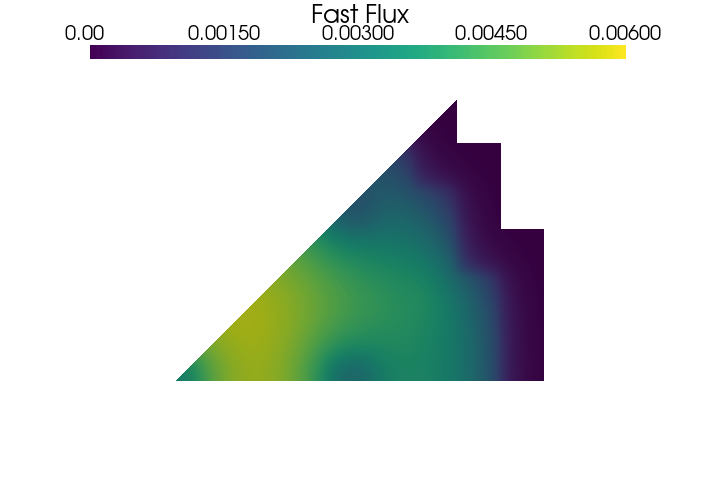
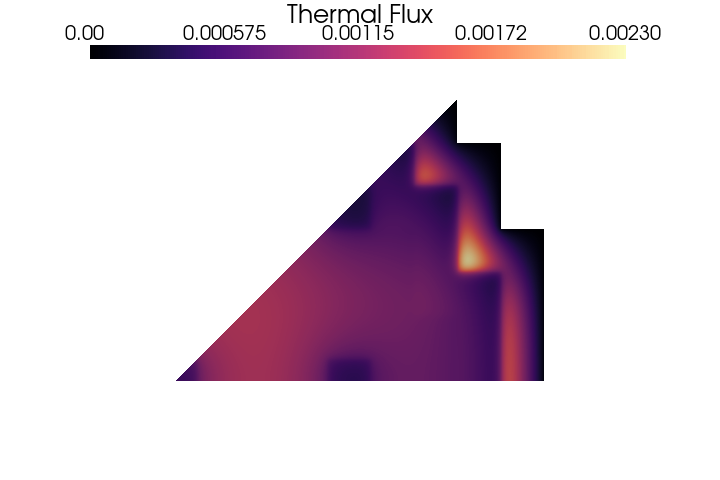
Let us know display the fluxes contour plots.
[11]:
from plotting import PlotScalar
import warnings
warnings.filterwarnings("ignore")
PlotScalar(phi_ss[0], show=True, varname='Fast Flux', resolution=[720, 480], clim=[0, 0.006], colormap=cm.viridis)
PlotScalar(phi_ss[1], show=True, varname='Thermal Flux', resolution=[720, 480], clim=[0, 0.0023], colormap=cm.magma)
[8]:
import pyvista as pv
from plotting import get_scalar_grid
from dolfinx.fem import Function
def subPlot_flux(fast: Function, thermal: Function,
filename: str = None, clim = None,
cmap1 = cm.viridis, cmap2 = cm.magma, resolution = [1400, 600]):
plotter = pv.Plotter(shape=(1,2), off_screen=False, border=False, window_size=resolution)
lab_fontsize = 20
title_fontsize = 25
zoom = 1.2
dict_cb = dict(title = ' ', width = 0.76,
title_font_size=title_fontsize,
label_font_size=lab_fontsize,
color='k',
position_x=0.12, position_y=0.86,
shadow=True)
clim_scale = .01
################### Fast Flux ###################
plotter.subplot(0,0)
if clim is None:
clim1 = [0, max(fast.x.array) * (1+clim_scale)]
dict_cb['title'] = 'Fast Flux'
plotter.add_mesh(get_scalar_grid(fast, varname='phi1'), cmap = cmap1, clim = clim1, show_edges=False, scalar_bar_args=dict_cb)
plotter.view_xy()
plotter.camera.zoom(zoom)
################### Thermal Flux ###################
plotter.subplot(0,1)
if clim is None:
clim2 = [0, max(thermal.x.array) * (1+clim_scale)]
dict_cb['title'] = 'Thermal Flux'
plotter.add_mesh(get_scalar_grid(thermal, varname='phi2'), cmap = cmap2, clim = clim2, show_edges=False, scalar_bar_args=dict_cb)
plotter.view_xy()
plotter.camera.zoom(zoom)
###### Save figure ######
plotter.set_background('white', top='white')
plotter.screenshot(filename+'.png', transparent_background = True, window_size=resolution)
plotter.close()
[9]:
# subPlot_flux(phi_ss[0], phi_ss[1], filename='anl11a2-contour')